螺旋錐齒輪是廣泛應(yīng)用于航空動(dòng)力傳動(dòng)及運(yùn)載工具等高端裝備中的核心基礎(chǔ)零部件，其高精密制造、加工誤差補(bǔ)償一直以來都是熱點(diǎn)難點(diǎn)問題。在實(shí)際加工中，機(jī)床的幾何誤差、跟隨誤差等因素導(dǎo)致螺旋錐齒輪加工誤差產(chǎn)生，對(duì)其接觸性能、使用壽命、傳動(dòng)精度產(chǎn)生諸多不良影響。Litvin等系統(tǒng)研究了加工參數(shù)變化對(duì)于螺旋錐齒輪嚙合特性等性質(zhì)的影響，提出了基于線性回歸算法的齒面優(yōu)化模型，但其求解精度穩(wěn)定性低、求解效率有待提高。為了增強(qiáng)求解穩(wěn)定性，Shih提出了序列二次歸納法，解決了雅克比矩陣的病態(tài)問題，但加工參數(shù)耦合作用導(dǎo)致的數(shù)值 求解不穩(wěn)定問題仍被忽略。Gabiccini及蔣進(jìn)科等基于齒面ease-off修正理論以準(zhǔn)雙曲面齒輪為研究對(duì)象，分別進(jìn)行了傳動(dòng)誤差變 化規(guī)律的研究及多目標(biāo)優(yōu)化設(shè)計(jì)的研究。李麗霞等從數(shù)學(xué)角度研究了加工參數(shù)與大輪齒面形狀的關(guān)系，但實(shí)際加工中通常不修正大輪，這一研究成果具有局限性。精密測(cè)量?jī)x器與技術(shù)的廣泛應(yīng)用，使螺旋錐齒輪加工誤差補(bǔ)償有了進(jìn)一步發(fā)展。唐進(jìn)元等基于三坐標(biāo)測(cè)量?jī)x，研究了銑削加工的螺旋錐齒輪齒面加工精度控制方法。丁撼等提出了考慮齒面微觀形貌的拓?fù)鋬?yōu)化方法，其提出了帶 Dog-leg步的置信域算法但其求解效率仍舊有待提高。彭山東等基于6δ原則探討了螺旋錐齒輪形性協(xié)同參數(shù)反調(diào)問題。以上研究雖然取得了一定進(jìn)展，但對(duì)螺旋齒錐齒輪雙重螺旋法加工齒面的高精度反調(diào)修正方法研究工作文獻(xiàn)較少、尚待深入研究。

　　本文通過建立螺旋齒錐齒輪雙重螺旋法加工精確數(shù)學(xué)模型，提出一種參數(shù)驅(qū)動(dòng)的雙重螺旋加工參數(shù)修正方法，并通過一對(duì)工程齒輪實(shí)際加工試驗(yàn)，驗(yàn)證了這一方法的可行性。本文方法可為螺旋錐齒輪加工參數(shù)反調(diào)提供幫助。

　　一、螺旋錐齒輪雙重螺旋法加工齒面建模

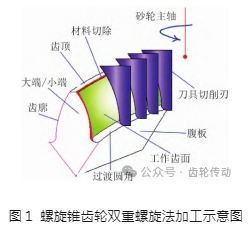
　　螺旋錐齒輪齒面建模是建立加工參數(shù)與齒面映射關(guān)系的過程。雙重螺旋法通過刀盤模擬“假想平頂齒輪”運(yùn)動(dòng)，由刀具切削刃在齒坯上形成齒形完成加工，如圖1所示。

　　基于坐標(biāo)變換，建立刀具與工件的坐標(biāo)轉(zhuǎn)換關(guān)系 Mbc。螺旋錐齒輪加工過程可以表示為

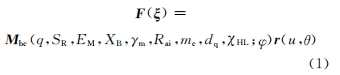
　　式中：F(ξ)為刀具在加工過程中形成的一系列曲面;r(u，θ)為刀具數(shù)字化表達(dá)，u為高度方向變量，θ 為回轉(zhuǎn)變量;φ為機(jī)床運(yùn)動(dòng)基本參數(shù)，表示刀具旋轉(zhuǎn)步長(zhǎng);ξ為螺旋錐齒輪雙重螺旋法的加工參數(shù)，ξ=[q，S_R，E_M ，X_D，X_B，γ_m，R_ai，m，j，χ_HL];q 為角向刀位;S_R 為徑向刀位;E_M 為垂直輪位;X_D 為水平輪位;X_B 為床位;γ_m 為安裝角;R_ai為刀轉(zhuǎn)角;m_c 為滾比;d_q 為刀具傾角;χ_HL為螺旋修正系數(shù)。根據(jù)嚙合原理，聯(lián)立方程組，螺旋錐齒輪雙重螺旋齒面參數(shù)化模型可以表示為

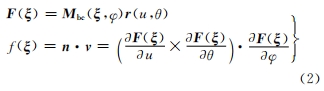
　　式中：n 為加工表面上任意一點(diǎn)的法矢;v為刀具與工件的相對(duì)速度;· 為標(biāo)量積符號(hào);× 表示矢量積符號(hào)。式(2)為螺旋主齒輪齒面隱式表達(dá)。將齒面投影范圍設(shè)置為邊界條件，通過合理的齒面均勻化手段，進(jìn)行齒面網(wǎng)格化處理，逐點(diǎn)求解。

　　二、參數(shù)反調(diào)修正優(yōu)化算法

　　齒面誤差控制模型

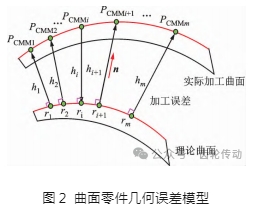
　　加工誤差是指刀具實(shí)際形成的包絡(luò)面與工件理論輪廓之間的偏差，圖2所示為曲面零件幾何誤差模型。基于精密測(cè)量技術(shù)對(duì)實(shí)際曲面進(jìn)行離散網(wǎng)格測(cè)量，得到實(shí)際加工曲面采樣點(diǎn) PCMM ，根據(jù)采樣點(diǎn)精確擬合出實(shí)際加工曲面。基于齒面參數(shù)化模型，離散化求解得到理論齒面點(diǎn)r₁，r₂，…，r_m，理論齒面點(diǎn)的擬合結(jié)果即為理論曲面，實(shí)際加工曲面與目標(biāo)曲面的法向距離h_m 即為加工誤差。

　　建立以機(jī)床加工參數(shù)為設(shè)計(jì)變量的曲面加工誤差模型

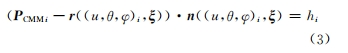
　　實(shí)際生產(chǎn)中，通常約束式 (3)中|h_i|≤0.005 mm。式(3)中：i表示第i 個(gè)采樣點(diǎn);r((μ，θ，φ)_i，ξ)、n((μ，θ，φ)_i，ξ)為采樣點(diǎn)對(duì)應(yīng)的理論曲面離散點(diǎn)徑矢及法矢

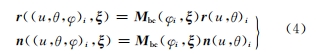
　　誤差補(bǔ)償策略

　　理論上，加工誤差是機(jī)床加工參數(shù)微小變化導(dǎo)致誤差的疊加，因此考慮加工誤差的真實(shí)齒面可以表示為

　　式中：ξ_e =ξ+Δξ= [q₀ +Δq，S_R0 +ΔS_R，E_M0 + ΔE_M0，X_D0 +ΔX_D，X_B0 +ΔX_B，γ_m0 +Δγ_m，R_ai0 + ΔR_ai，m₀+Δm，j₀+Δj，χ_HL0+Δχ_HL]。通過調(diào)整加工參數(shù)可以實(shí)現(xiàn)齒面加工誤差的補(bǔ)償，然而優(yōu)化變量過多會(huì)降低誤差補(bǔ)償效率。采用敏感性分析方法定量描述加工參數(shù)對(duì)加工誤差的影響，制定合理的優(yōu)化策略非常必要。這一定量描述通常被稱為敏感性系數(shù)，參數(shù)敏感性系數(shù)越大，對(duì)模型輸出影響越大。基于 Morris法評(píng)估加工參數(shù)敏感性，通過對(duì)加工參數(shù)進(jìn)行多次隨機(jī)變化采樣，計(jì)算并求其平均值，用來評(píng)估其敏感性。本文采用齒面誤差控制模型輸出對(duì)輸入變量的一階偏導(dǎo)數(shù)與對(duì)應(yīng)法矢的點(diǎn)乘結(jié)果作為敏感系數(shù)

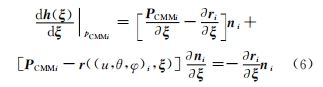
　　式中：i∈[1，n]，n 為曲面離散點(diǎn)數(shù)量。對(duì)式(6)進(jìn)行計(jì)算，得到全部曲面點(diǎn)關(guān)于各項(xiàng)機(jī)床參數(shù)的敏感系數(shù)組成的雅克比矩陣，稱為曲面采樣點(diǎn)隨各項(xiàng)加工參數(shù)變化的敏感系數(shù)矩陣

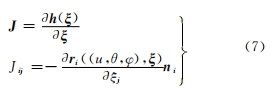
　　式中：j∈[1，m]，m 為機(jī)床設(shè)置參數(shù)數(shù)量。幾何誤差模型可改寫為

　　為便于排序，求每一個(gè)機(jī)床參數(shù)的綜合敏感系數(shù)，可得

　　對(duì)綜合敏感系數(shù)進(jìn)行排序，選取敏感性最大的 3～5個(gè)的加工參數(shù)作為優(yōu)化變量。由于雙重螺旋法加工過程中，凹凸面具有較強(qiáng)的耦合效應(yīng)，在制定優(yōu)化策略時(shí)優(yōu)先考慮工作面(通常為小輪凹面與大輪凸面)的參數(shù)敏感性。

　　參數(shù)反調(diào)優(yōu)化算法

　　式(3)具有強(qiáng)烈的非線性方程性與超越穩(wěn)定性，為了克服求解 min(h)時(shí)非線性特性導(dǎo)致雅克比矩陣病態(tài)或奇異引起的求解不穩(wěn)定問題，將式(3) 表達(dá)成非線性最小二乘問題

　　考慮到螺旋錐齒輪誤差補(bǔ)償問題的強(qiáng)烈非線性特性，為了提高結(jié)果穩(wěn)定性，以改進(jìn)的 L-M 方法作為優(yōu)化算法。基本思路是在每一次迭代時(shí)求解

　　式中：Δξ_k+1、Δξ_k 分別為第k+1次循環(huán)和第k次循環(huán)求得的反調(diào)量;F_k 為 第k次循環(huán)的目標(biāo)函數(shù)值(即預(yù)測(cè)誤差);J_k 為第k次循環(huán)的敏感系數(shù)矩陣;λ_k 是為了克服J_k^TJ_k 所帶來不良矩陣的非負(fù)參數(shù)。

　　L-M 方法有線搜索及信賴域搜索兩種搜索思想。本文基于信賴域搜索思想，在每次迭代時(shí)，在當(dāng)前迭代點(diǎn)的信賴域內(nèi)找到一個(gè)試探解，這一解將用于反饋調(diào)節(jié)信賴域。值得注意的是，L-M 方法通過調(diào)節(jié)迭代參數(shù)λ_k間接調(diào)節(jié)信賴域半徑，選取合理的迭代參數(shù) λ_k有利于其發(fā)揮作用。Yamashita 和 Fukshima提及過可以選取λ_k=‖F(xiàn)_k‖² 的方式，而Fan和 Yuan則選取λ_k=‖F(xiàn)_k‖。固定的信賴域調(diào)節(jié)系數(shù)會(huì)給求解帶來問題，當(dāng)加工精度調(diào)整到接近最優(yōu)解集時(shí)，λ_k 容易因?yàn)檫^小而失去作用。引入阻尼系數(shù)μ，增強(qiáng) λ_k 的調(diào)節(jié)作用。當(dāng)加工精度接近目標(biāo)值，借助阻尼系數(shù)放大迭代參數(shù)，使求解更穩(wěn)定。從實(shí)際下降量與模型下降量的匹配程度及當(dāng)前精度與目標(biāo)值的距離兩方面來更新阻尼系數(shù)，以完成迭代參數(shù)λ_k 的評(píng)價(jià)和控制，定義如下

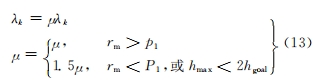
　　式中：r_m 為實(shí)際下降量與模型下降量之比;h_max = max(h_i)，表示曲面殘余誤差最大值;hgoal為優(yōu)化目標(biāo)，即預(yù)設(shè)曲面最大誤差。在進(jìn)行優(yōu)化參數(shù)計(jì)算時(shí)還考慮以下3個(gè)問題：一是確保修正后的加工參數(shù)可用于實(shí)際加工，需要在避免傳統(tǒng) L-M 方法導(dǎo)致的過度調(diào)整，采取2個(gè)舉措(①識(shí)別越界參數(shù)，將其賦值為上一次迭代結(jié)果;② 在優(yōu)化策略中去除該參數(shù));二是在計(jì)算過程中，傾向于選擇誤差最大值減小的結(jié)果，所以對(duì)于信賴域半徑的調(diào)節(jié)要進(jìn)行綜合考慮;三是為了平衡控制精度、效率與穩(wěn)定性，需要根據(jù)初始誤差設(shè)置優(yōu)化精度。

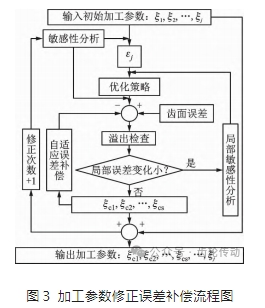
　　加工參數(shù)修正誤差補(bǔ)償流程

　　加工參數(shù)修正基本流程如圖3所示。第一步，輸入原始加工參數(shù)。第二步，進(jìn)行算法初始化，根據(jù)誤差模型進(jìn)行加工參數(shù)敏感性分析，得到每一個(gè)加工參數(shù)的綜合敏感性系數(shù)ε_j，進(jìn)行排序;接著將敏感性強(qiáng)的s(通常取3～5)個(gè)參數(shù)以變量形式計(jì)入優(yōu)化方案，保留敏感性較弱的參數(shù);制定出優(yōu)化策略。第三步，利用參數(shù)反調(diào)算法進(jìn)行精確求解，求解完成后需要對(duì)當(dāng)前優(yōu)化結(jié)果進(jìn)行驗(yàn)證，需要檢查當(dāng)前加工參數(shù)是否溢出邊界，能否滿足加工要求;在此基礎(chǔ)上，還需要檢查是否存在局部誤差補(bǔ)償能力不足的情況，若存在，則需進(jìn)行局部敏感性分析，調(diào)整優(yōu)化策略;最后將優(yōu)化后的參數(shù)與保留參數(shù)以矩陣形式統(tǒng)一輸出，稱為補(bǔ)償后的加工參數(shù)。在反復(fù)調(diào)整加工參數(shù)以達(dá)到補(bǔ)償加工誤差的過程中，可以選擇更多的加工參數(shù)參與誤差補(bǔ)償提高算法的誤差補(bǔ)償能力。

　　三、結(jié)果與討論

　　算例

　　以工程實(shí)際中一對(duì)高精度螺旋錐齒輪副作為應(yīng)用實(shí)例，表1為該對(duì)齒輪的初始加工參數(shù)，包含刀盤參數(shù)和機(jī)床加工參數(shù)。通過修正機(jī)床加工參數(shù)完成補(bǔ)償加工誤差。

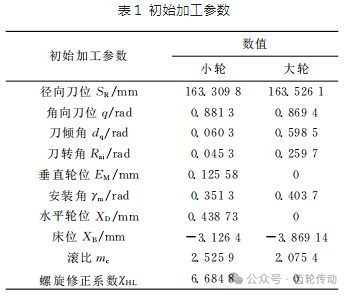
　　圖4為小輪齒面離散點(diǎn)，包含工作面和根尖圓角兩部分，藍(lán)色部分為工作齒面區(qū)域，紅色部分為齒根圓角區(qū)域。圖中顯示雙重螺旋法加工一次加工形成的完整齒槽的凹凸兩面。圖 5 為齒輪副三維模型：圖5a、圖5b分別為小輪、大輪三維模型;圖5c為齒輪副裝配模型圖。

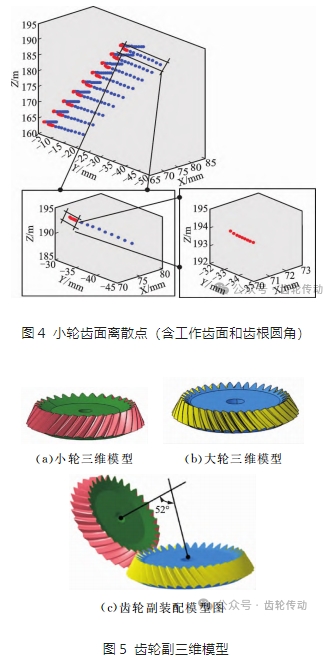
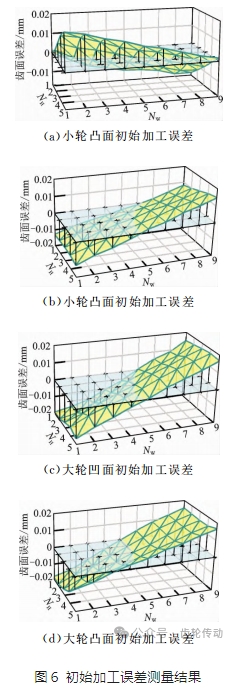
　　圖6為初始加工誤差測(cè)量結(jié)果，其中 N_H 為沿齒高方向齒面點(diǎn)編號(hào)，N_W 為沿齒寬方向齒面點(diǎn)編號(hào)。圖6a、6b分別為小輪凸面、凹面誤差測(cè)量結(jié)果;圖6c、6d分別為大輪凸面、大輪凹面誤差測(cè)量結(jié)果。

　　優(yōu)化結(jié)果及討論

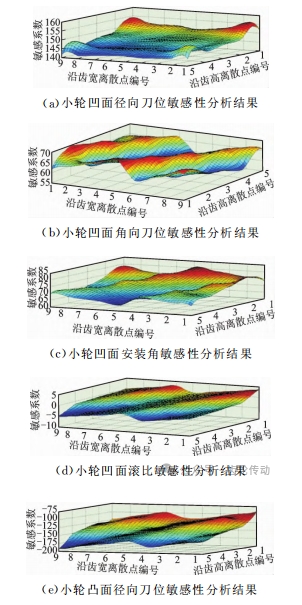
　　對(duì)初始加工參數(shù)進(jìn)行敏感性分析，選擇優(yōu)化變量。由于螺旋錐齒輪齒面形狀較為復(fù)雜，為了讓最終的敏感性分析結(jié)果充分體現(xiàn)出該參數(shù)對(duì)全齒面的影響力，選擇齒面上5×9個(gè)齒面點(diǎn)求敏感系數(shù)，構(gòu)成敏感系數(shù)矩陣。

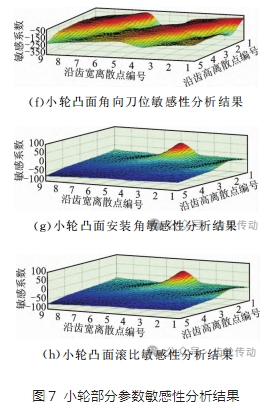
　　圖7為部分加工參數(shù)的敏感性分析結(jié)果，雙重螺旋法同時(shí)加工兩側(cè)齒面，需要考慮兩側(cè)齒面對(duì)于加工參數(shù)的敏感性。由圖5可知，對(duì)于小輪，加工參數(shù)對(duì)齒面不同點(diǎn)的影響能力有所區(qū)別，凹凸面兩側(cè)的敏感性也不同。徑向刀位增大會(huì)導(dǎo)致凹面全齒面誤差增大，凸面誤差減小，按照優(yōu)先修正凹面加工誤差的原則，在修正時(shí)選擇徑向刀位增大的方向;角向刀位增大，凹面加工誤差均增大，凸面加工誤差趨勢(shì)相反;安裝角增大，凹凸面加工誤差均增大，且其影響能力對(duì)凹面加工誤差更強(qiáng);滾比對(duì)齒頂與齒根兩個(gè)方向的齒面點(diǎn)齒面誤差敏感性更強(qiáng)。

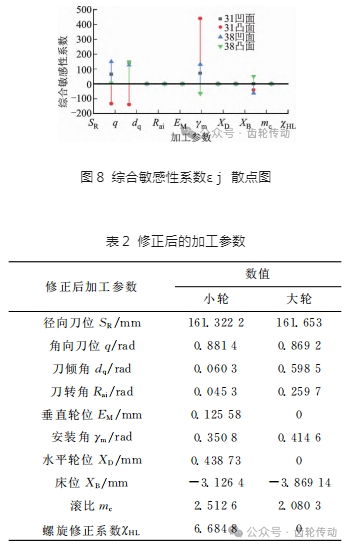
　　按照式(8)計(jì)算綜合敏感性系數(shù)ε_j，繪制散點(diǎn)圖如圖8所示，可以觀察到徑向刀位(S_R)、角向刀位(q)、安裝角(γ_m)、滾比(m)對(duì)應(yīng)的敏感系數(shù)偏離零點(diǎn)更遠(yuǎn)，具有更大的敏感性，故作為本次優(yōu)化過程中的優(yōu)化變量。經(jīng)過調(diào)整優(yōu)化后的加工參數(shù)如表 2 所示。

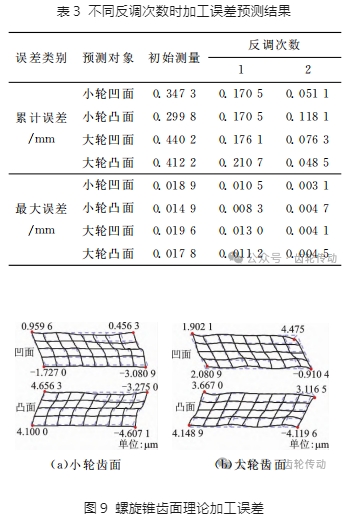
　　本文分別從累計(jì)誤差的下降量及最大誤差下降量來評(píng)估誤差補(bǔ)償效果，預(yù)測(cè)殘余誤差的統(tǒng)計(jì)結(jié)果如表3所示。由表3可見：第一次反調(diào)后，累計(jì)誤差與最大誤差均減小，但最大誤差大于0.005mm 不符合實(shí)際需求;兩次反調(diào)后小輪凹、凸面累計(jì)誤差分別減少了85.29%和60.59%，最大誤差分別減少了 83.7%和68.75%;大輪凹、凸面累計(jì)誤差分別減少 了 82.66% 和 88.02%，最大誤差分別減小了 78.79%和75%，說明該方法有效。圖9為螺旋錐齒輪齒面理論加工誤差擬合圖，可以看到擬合后的殘差曲面均勻連續(xù)，齒面殘余誤差均能控制在 0.005mm 內(nèi)。

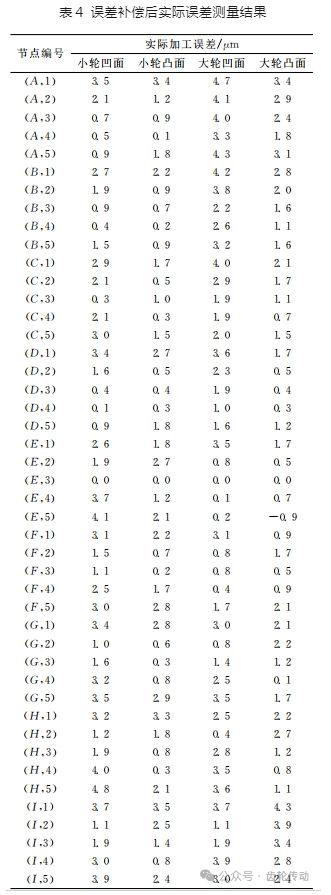
　　用補(bǔ)償后的加工參數(shù)進(jìn)行加工驗(yàn)證，如圖10所示。基于格里森測(cè)量機(jī)對(duì)加工誤差進(jìn)行測(cè)量，實(shí)際齒面誤差測(cè)量結(jié)果如圖11所示。圖11為網(wǎng)格劃分示意圖，表4為加工參數(shù)修正后小輪、大輪的實(shí)際誤差測(cè)量結(jié)果。與優(yōu)化前測(cè)量結(jié)果對(duì)比，可知小輪凹面、凸面加工誤差最大值分別為3.5μm、4.8μm，降低了81.5%、67.8%;大輪凹面、凸面加工誤差最大值分別為4.3μm、4.7μm，降低了78.1%、73.6%。齒面誤差得到了有效減小，滿足實(shí)際工程需求。

　　四、結(jié)論

　　本文提出了針對(duì)螺旋錐齒輪雙重螺旋加工的一種加工誤差控制方法，通過加工參數(shù)反調(diào)來補(bǔ)償加工誤差;基于改進(jìn)的 L-M 算法建立加工參數(shù)優(yōu)化算法，克服了傳統(tǒng)方法中雅克比矩陣病態(tài)或奇異的問題;根據(jù)加工誤差對(duì)不同加工參數(shù)的靈敏度，選擇合適的加工參數(shù)進(jìn)行優(yōu)化，有效提高了優(yōu)化效率。從優(yōu)化結(jié)果分析可以看出：本文方法能夠高效地實(shí)現(xiàn)螺旋錐齒輪磨削加工精度的控制與優(yōu)化，能在較少的反調(diào)次數(shù)內(nèi)，有效提高實(shí)際加工齒面與理論設(shè)計(jì)齒面的貼合程度;通過調(diào)整加工參數(shù)對(duì)加工誤差進(jìn)行補(bǔ)償后，最大殘余誤差不超過5μm，得到滿足實(shí)際磨齒加工需求的加工參數(shù)。本文工作為雙重螺旋法螺旋錐齒輪齒面高精度加工提供了一種誤差補(bǔ)償新思路，在理論方法與工程應(yīng)用上均有一定參考價(jià)值。

　　參考文獻(xiàn)略.